Mike Roth
Mathematics and StatisticsQueen's University, Kingston,
Ontario, Canada, K7L 3N6
Tel: 613-533-2410

Mike Roth
Department of Mathematics and StatisticsMike Roth
Mathematics and Statistics

| 15. | Codimension two integral points on some rationally connected threefolds are potentially dense (with David McKinnon). J. Algebraic Geom.31 (2022), 345—386. |
| Let X be a smooth rationally connected threefold defined over a number field k, and Z a closed subset of X of codimension at least 2. In this paper we show that for many such X there is a finite extension K of k such that the Z-integral points of X(K) are Zariski dense. This answers a question of Hassett and Tschinkel from 2001. | |
| 14. | Intersection Multiplicity One for Classical Groups (with Ivan Dimitrov). Transformation Groups 49 (2019), 1001—1014. |
| This paper shows that when G is a classical group the structure coefficients of the Belkale-Kumar product on G/B are all 0 or 1. | |
| 13. | Positive Systems of Kostant Roots (with Ivan Dimitrov). Algebras and Representation Theory 20 (2017), 1365—1378. |
| This paper establishes a result on Kostant root systems for classical simple Lie algebras, addressing the question of when a subset of Kostant roots is contained in a positive system. This result is needed for an application in 7. | |
| 12. | An analogue of Liouville's theorem and an application to cubic surfaces (with David McKinnon). European Journal of Mathematics 2 (2016), 929—959. |
| In this paper we generalize, in the sense of 11, Liouville's approximation theorem to arbitrary varieties, as well as giving an extension involving the asymptotic base locus. As an application, we compute εx(L) and αx(L) for all nef line bundles L on a cubic surface, and all points x not on a line. | |
| 11. | Seshadri constants, Diophantine approximation, and Roth's theorem for arbitrary varieties (with David McKinnon), Inventiones Mathematicae 200 (2015) 513—583. |
| Let X be a variety defined over a number field k. The Bombieri-Lang conjecture is a prediction that global positivity of the canonical bundle of X implies a global limitation on the accumulation of rational points. In this paper we investigate local versions of this predicted phenomena. Given a line bundle L and point x ∈ X, the main theme of the paper is the interrelations between εx(L), the Seshadri constant, measuring local positivity of L at x, and αx(L), an invariant measuring the accumulation of rational points at x, as gauged by L. The two invariants share similar formal properties. Moreover the classic approximation results on the affine line — the theorems of Liouville and Roth — generalize as inequalities between αx and εx valid for all projective varieties. | |
| 10. | Decomposing Inversion Sets of Permutations and Applications to Faces of the Littlewood-Richardson Cone (with Rian Dewji, Ivan Dimitrov, Adam McCabe, David Wehlau, and Jenny Wilson), J Algebr Comb 45 (2017), 1173–1216. |
| This paper solves the problem, in types A, B, and C, of producing elements (w1,w2,…,wk) of the Weyl group whose inversion sets partition the set of positive roots. Such collections of group elements are the combinatorial information appearing in the solution of Problem I in 7. We use this recursive description to answer some enumerative questions and prove that certain faces of the Littlewood-Richardson cone are simplicial. The paper also discusses a useful way to visualize inversion sets. | |
| 9. | Reduction rules for Littlewood-Richardson coefficients, International Mathematics Research Notices, Vol 2011, No. 18, 4105–4134. |
| This paper shows that every regular face of the
Littlewood-Richardson cone of a semisimple group G gives rise to a |
|
| 8. | Geometric realization of PRV components and the Littlewood-Richardson cone (with Ivan Dimitrov), Contemp. Math. 490, Amer. Math. Soc. Providence, RI 2009, 83–95. |
| This paper is a mostly expository discussion of the main questions (and some of the answers) in 7, written from the point of view of representation theory. The paper was written while the previous article was in preparation and as a result some of the problems raised here are solved in 7. | |
| 7. | Cup products of line bundles on homogeneous varieties and generalized PRV components of multiplicity one (with Ivan Dimitrov), Algebra & Number Theory 11-4 (2017), 767—815. |
| Let X=G/B be a complete flag variety. The two main questions answered by this paper are when the cup product of cohomology groups of line bundles on X is surjective, and which irreducible G-representations of a tensor product can be realized by such a surjection. | |
| 6. | Abel-Jacobi Maps Associated to Smooth Cubic Threefolds (with Joe Harris and Jason Starr), arXiv:math.ag/0202080 |
| This paper studies the Abel-Jacobi map from the space Hg,d(X) of degree d, genus g curves on a smooth cubic threefold X to the intermediate Jacobian of X, and proves that this map coincides with the maximally rationally connected fibration of Hg,d for d < 6. | |
| 5. | Curves of Small Degree on Cubic Threefolds (with Joe Harris and Jason Starr), Rocky Mountain Journal of Mathematics 35 (2005) 761–818. |
| This paper contains prepatory results needed for paper 6 on the study of the Abel-Jacobi map on cubic threefolds. It proves that for any smooth cubic threefold the space parameterizing degree d, genus g, curves is irreducible of the expected dimension, for d < 6. | |
| 4. | Inverse Systems and Regular Representations, Journal of Pure and Applied Algebra 199 (2005) 219–234. |
| This paper generalizes a result used in algebraic combinatorics when studying reflection groups and gives a conceptual explanation in terms of Grothendieck duality. | |
| 3. | The Affine Stratification Number and the Moduli Space of Curves (with Ravi Vakil), Centre de Recherches Mathématiques Proceedings and Lecture Notes, Volume 38 (2004) 213–227. |
| This paper introduces the idea of the affine stratification number of a scheme, develops its basic properties, and shows how it can be used to bound the topological complexity of the scheme. | |
| 2. | Rational Curves on Hypersurfaces of low degree (with Joe Harris and Jason Starr), Journal für die reine und angewandte Mathematik (Crelle's Journal) 571 (2004) 73–106. |
| This paper proves that for a general hypersurface of degree d < (n+1)/2 in Pn the scheme parameterizing degree e rational curves in the hypersurface is a complete intersection of the expected dimension for all e. | |
| 1. | Stable maps and Quot Schemes (with Mihnea Popa), Inventiones Mathematicae 152 (2003) 625–663. |
| This paper uses stable maps to construct an alternate compactification of the space of vector bundles quotients of a fixed vector bundle, and applies this to obtain results about the Quot scheme. |
|
Math 413/813 : Introduction to Algebraic Geometry.
(Winter 2015) An first course in algebraic geometry. |

|
Math 210: Introduction to abstract algebra.
(Winter 2008) A first course in abstract algebra. |
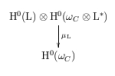
|
Introduzione alla teoria di Brill-Noether.
(Inverno 2007) Corso di dottorato tenuto alla università Roma III. |
|
Math 819: Introduction to Algebraic Geometry.
(Fall 2005) An incomplete introduction to Algebraic Geometry. |
|
Math 120: An introduction to calculus.
(Fall 2022–Winter 2023) An introduction to calculus with ε's and δ's. |
 |
Math 121: Differential and Integral Calculus. (Winter
2004) Second semester in a standard calculus sequence. This page was created in order to distribute some extra handouts. The rest of the course information was on the official home page. |

|
Math 419/819: Algebraic Curves and Riemann Surfaces. (Fall 2003)
An introduction to some of the basic facts about Algebraic Curves/Riemann Surfaces. |
| The math club meets weekly, from 5:30–6:30 on Thursdays, in Jeff 118. Each week we talk about an interesting topic in mathematics. Follow the exclamation mark to see the schedule. |

|